Absolute Extrema

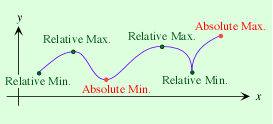
When you are looking at a graph, sometimes it is very easy to determine where the highest point is, what we will refer to as the absolute maximum, and the lowest point in the graph, which we will refer to as the absolute minimum.

For instance, the graphs below, which are all on a closed intervals, [a,b], each contain a maximum and a minimum.

The first graph in linear and contains a min at a and a max at b.
In the second graph, the max is between points a and b and the minimum is b.
The final graph shows the max and the min in between a and b.

So, you can also have a crazy graph with many dips and peaks. When a graph changes from increasing to deceasing, or vice versa, at a point with a horizontal slope, this is also known as a max or min, but these are referred to as relative maximums or relative minimums. Sometimes these same points are referred to as local max or mins.

In this post though we are focusing on the ABSOLUTE MAXIMUM and the ABSOLUTE MINIMUM, which are the highest and lowest y-values displayed on the graph. But, what if we are given a function without the accompaniment of a graph? How do we evaluate the absolute min and max then? YOU GUESSED IT!!!

BY USING THE DERIVATIVE, OF COURSE!!!!!

We could use a first derivative sign chart to help us begin, but ultimately, the chart gives us the zeros of the graph, and we still have to know if these zeros (critical values/horizontal tangent lines/points on the graph) are the absolute max and absolute min, as they could be just relative max or mins.

In order to do this, we are given a function, take the function’s derivative, set it equal to zero, solve, and then evaluate all the critical values and intervals inside the original equation to determine the highest and lowest output. Easier said than done, huh?

Let’s try some examples.

$f(x)= x^3-6x^2+9x-8$ on the interval $[0,5]$
Take the derivative.
$f'(x)= 3x^2-12x+9$
Set the derivative equal to zero and solve.
$3x^2-12x+9=0$
Factor out a 3.
$3(x^2-4x+3)=0$
$3(x-1)(x-3)$
$(x-1)=0$
$(x-3)=0$
$x=1$ and $x=3$
So, we have to test the critical values, which are our zeros, 1 and 3.
And, we have to test the interval values, 0 and 5.
Don’t forget! We are checking these values back in the ORIGINAL equation.

The original equation: $f(x)= x^3-6x^2+9x-8$
$(1)^3-6(1)^2+9(1)-8=-4$
$(3)^3-6(3)^2+9(3)-8=-8$
$(0)^3-6(0)^2+9(0)-8=-8$
$(5)^3-6(5)^2+9(5)-8=12$

So, from this information, we can conclude the ABSOLUTE MAX is 12 when $x=5$ .
There are two values that produce the same minimum value, so we have two mins. The ABSOLUTE MIN is -8 when $x=0$ and when $x=3.$

Let’s do another:

$f(x)=x^4-32x^2-7$ on the interval $[-5,6]$
Take the derivative.
$f'(x)=4x^3-64x$
Set the derivative equal to zero.
$f'(x)=4x^3-64x=0$
Factor out 4x.
$4x(x^2-16)$
$4x(x-4)(x+4)$
$4x=0$
$(x-4)=0$
$(x+4)=0$
Therefore, this time our critical values to check are: 0,-4, and 4.
Don’t forget our interval values: -5 and 6.
AND–That’s right use the ORIGINAL FUNCTION!!

$(0)^4-32(0)^2-7=-7$
$(4)^4-32(4)^2-7=-263$
$(-4)^4-32(-4)^2-7=-263$
$(-5)^4-32(-5)^2-7=-182$
$(6)^4-32(6)^2-7=137$
Therefore, the absolute maximum is 137 at x=6.
And, the absolute minimum is -263 when x=4 and x=-4.

Finally, let’s finish with one that is a little more challenging.

$f(x)= (x^2+4)^\frac {1}{3}$ on the interval $[-2,2]$ .
First, let’s take the derivative.
This function will need the use of the power rule and the chain rule to take the derivative.
$f'(x)= \frac {1}{3}(x^2+4)^- \frac {2}{3} \cdot (2x)$
Let’s rewrite our derivative, so that we put the negative exponent in the denominator of a fraction as we really don’t like working with negative exponents.
$\dfrac {2x}{3(x^2+4)^ \frac {2}{3}}$
Doesn’t that just LOOK so much nicer!!
Now, set that REWRITTEN derivative equal to zero.
$\dfrac {2x}{3(x^2+4)^ \frac {2}{3}}=0$
When we solve, we find that:
The absolute minimum is about 1.58 at x=0.
The absolute maximum is 2 at x=-2 and x=2.

Hey, it’s Sunday, I’m watching football, MY TEXANSSSS just got another touchdown, it’s the first day of my favorite month, lets do ONEEE MORE!

$f(x)= \dfrac {x}{x^2+1}$
To take the derivative, use the quotient rule.
$f'(x)= \dfrac {(x^2+1)(1)-x(2x)}{(x^2+1)^2}$
Simplify.
$f'(x)= \dfrac {x^2+1-2x^2}{(x^2+1)^2}$
$= \dfrac {1-x^2}{(x^2+1)^2}$
$= \dfrac {(1+x)(1-x)}{(x^2+1)^2}$
Set the numerator equal to zero.
$(1+x)=0$
$(1-x)=0$
The critical values are x=-1 and x=1.
Plug the critical values back into the original equation to find the absolute maximum and absolute minimum.
The absolute max is .5 when x=1.
The absolute min is -.5 when x=-1.