Reflecting!! Calculus 2321 and THE BLOG PROJECT!

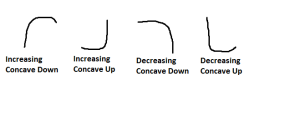
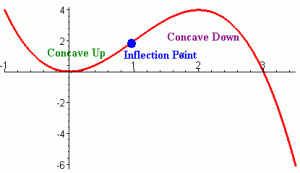
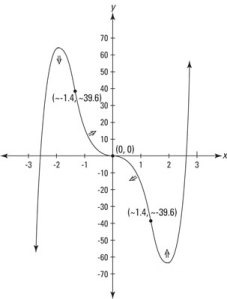
Calculus has always been very challenging for me. In fact, this is not my first, or even second time to attempt it in college. I am graduating in less than 2 weeks, and I held off taking this DAMNED class for as long as possible as I was afraid to fail AGAIN. In high school, I was a “smart” student without attempting much effort, and college wasn’t much difference with the EXCEPTION of CALCULUS 2321. Since this was my last semester, and according to my mother, “the last straw,” I knew I had to give this class everything I had! And I’ve never learned more. This attempt, I looked for a teacher with a different style of teaching. Luckily, I was in a very small class, so receiving one-on-one help was POSSIBLE and my teacher encouraged group work. She rarely got before the entire class and just lectured, and then assigned countless problems to be worked out of the book, in fact she NEVER did. She created individual and unique lessons that she introduced topics directly to the class, but then it was up to us and our group to figure out HOW to do the work. She would then walk around the classroom while this occurred, and cleared up misconceptions as she heard them. Finally, we would go over several examples as a class, just to make sure everyone was on the same page. Our homework was assigned online with a program called MathXL. I liked this program as I could have it show me how to solve the problem step-by-step if I was confused and gave me similar exercises so I could rework the examples over and over and it was very BENEFICIAL practice. Normally, I would have had a problem from a book, and if I didn’t know where to start, I would instantly give up. And they say, Practice makes perfect, right?

Although I still struggled with the multiple choice tests given in this class, I thoroughly enjoyed the assigned blog project as it gave me an opportunity to use my creative side as well as learning valuable skills for the future. I loved having the freedom to chose the topics of my posts and how often I wanted to post them. I also enjoyed learning how to code in latex and feel this may be a useful skill to know if I ever want to make worksheets for math in the future. Not to mention, I learned how to set up and start my own blog, something I have always wanted to do!! (I never dreamed the first one would be about Calculus!! But- heyyyy!) Several times, I would have my friends ask me what kind of homework I was doing, and I would simply respond, “I have to Blog for Calculus!” You should have seen some of the confused looks I would get! “How do you blog about Calculus?!?!” “A MATH BLOG?!?!” “Why would you be blogging?!” And very proudly, I would whip out my phone, open my downloaded WordPress App, and show them my blog I’ve spent COUNTLESS hours on to make informative, entertaining, and yes, somewhat, “pretty”!

I really enjoyed this class and I really enjoyed posting in this blog, unfortunately, as it was a REQUIRED assignment, and this last post suffices the course’s requirements: This is goodbye from THE BIG C.

Hope you learned a lot through my posts!!

Eat Em Up!

Kori 🙂

NEW Home! New Fence!

So, in my last post, we figured out the dimensions needed to maximize the area in my pig pen. Today, I’ve built a new house along the gorgeous San Marcos River, so my yard needs a fence. Since the river IS my backyard, we only need to build a fence with three sides. We have 2400 feet of fencing and want to fence off my yard that borders the straight river behind my house. What are the dimensions of my yard that gives me the largest area?

Let’s draw a picture first.

Now, we need a mathematical formula to MAXAMIZE my area of my yard.
So, let’s use the area formula: A=xy
We do have a couple of constraints, our 3 sides and total amount of fencing we have to use.
So, mathematically our constraint is:

Now, we want to solve our second equation for y. Then we will substitute the result into the first equation to express A as a function of one variable.





To find the absolute maximum value, we use the closed interval method. To do so:
1. We must find the values of f at critical numbers of f in (a,b)
2. Find the values of f at the end points of the interval.
3. Then the largest value from steps 1/2 is the ABSOLUTE MAX and the smalles value is the ABSOLUTE MIN.

Remember, we’re building a fence, so our dimensions must be

Find the derivative.

To solve for critical numbers, solve the equation.

x=600
To find the MAX VALUE, evaluate the endpoints and critical numbers into the original equation..



Therefore, the max value is when x=600 and is 720,000 square feet.
The dimensions then are 600×1200 which keeps in line with our constraint.
To get our y dimension (the length), when you find the value of x, you simply plug it back into the equation when y is isolated.

Well, I’ve got a lot of fence to start building!

Learn something new every day!

Kori 🙂

Hey Yall!

So, I have written several posts on how we can continue to use Calculus and the use of the derivative in real world applications! It’s always more fun learning something that one can relate to. So, I don’t know if you’re a farmer, but if you are, you’re in luck! Today, we are going to learn how to make the largest PIG PENS POSSIBLE! (Showing off my sweet alliteration skills, and no, we’re not talking about my ROOM!!! )

We want to build a rectangular pig pen with three parallel partitions using only 500 feet of fencing.

So, we want something that kind of looks like this picture above.

What dimensions will maximize the total area of the pig pen?

So, let’s begin by looking at our cute pen a little more mathematically!
We want to think about the largest possible dimensions to have with only 500 ft of fencing, which is our constraint.
The length and width of the fence are what we are manipulating, therefore they are our variables, so let’s label them. Drawing pictures always makes word problems easier to HOE DOWN YALL!

So, now what?
Well, in my picture I labeled my width of my fence as x and my length as y.
We need to now use this information and the information given to us in the problem to come up with an equation.
So, we have five widths, which we will multiply, two length sides, which will also be multiplied, and a constraint of 500 feet for the total amount of fencing, and we want to MAXAMIZE the total area of our pen.

So, 500= 5(width)+2(length), which is equal to 5x+2y.
Let’s rearrange this equation to get only one variable inside our equation. (Makes life WAY easier!)

Solve to get y alone.

So we need to use this equation we have created with the equation for area.
Area= Length Width
A=xy
Now, plug in our new y into the Area Equation.

Now let’s distribute the x.

Now!! We’re going to do Calculus to find our maximum area for our little piggies!
So, like always, let’s differentiate our equation we’ve created above.

We can simplify,

Now, let’s set this bad boy equal to zero to solve for our critical values.
Easiest thing to do first is factor out what is in common.


Solve.
x=50
Now, that we have an x value, we can plug it back into our equation that has y isolated on one side and solve for y.
Then we will plug in our x and y variable into the area equation to get our MAX possible area!

y=125
A=(50)(125)
A=6,250 sq feet is the maximum possible area of our pig pen with the largest possible dimensions with three parallel partitions. The dimensions are 50 feet by 125 feet.

Hope ya’ll had a good time learning!!!

Learn something new everyday!!

Kori 🙂

Curve Sketching

If you have been keeping up with my posts, then you will truly appreciate this one as it combines MANY skills we’ve learned to allow us to sketch these different functions based on their derivatives, which tell us our critical values, which are the points on the graph which have a horizontal tangent line. The first derivative can also be solved to find local max and mins. We will use inflection points obtained from the second derivative, which tell us if our graph is changing from concave up or concave down.

Let’s get started!!!

The function for our normal polynomial graph is:

From this equation, we can consider the domain which is .
The y-intercept is located at
Next, let’s find the derivative, and then the critical values when the derivative is equal to zero.


Factor out the 6.


So, x=2 or x=-1.
Now, let’s use these critical values and place them on a first derivative sign chart.

-To make this sign chart, we plotted our critical values found from the first derivative, then tested numbers from each region to determine if the function is increasing or decreasing. So, the chart shows that f(x) is increasing on and and is decreasing on (-1,2).
-We can also decide where our relative max and mins are from the sign chart. The relative maximum is at x=-1 and the relative minimum is x=2.. When we plug these values baack into our equation we can get the y-values. The relative maximum f(-1)= 8 and the relative minimum is f(2)=-19.

Now, we’re going to use the SECOND DERIVATIVE to dertermine the intervals where the function is concave upward or downward. So the second derivative is the derivative of the first derivative which is:

Set this equal to zero and
Once again, we will make a sign chart, this time for the second derivative to test points on either side of

When we tested a point less than the chart shows that the function is concave down on because it is negative, and it is concave upward on because it is positive.

The second derivative also shows us our inflection points, which, if you remember, are the points in which the concavity CHANGES. The inflection point is at

Now, we can use all this knowledge to sketch our graph.

First, I plotted my points. Then I decided if the function was increasing or decreasing between intervals, then if it were concave up or down according to my sign charts and this graph is a result of the function.

I hope this helps you to sketch future graphs!

Learn something new every day!!

Kori 🙂

Derivative of a Logarithmic Function (In the REAL WORLD!!)

Like in my last blog, I am going to show you how we can once again use calculus, the derivative specifically in a real world situation. This application problem comes from the textbook, Calculus for Life Sciences: Greenwell, Ritchey, and Lial, Section 4.5 problem number 48.

Insect Mating!
Consider an experiment in which equal numbers of make and female insects of a certain species are permitted to intermingle. Assume that:

represents the number of matings observed among the insects an hour, where t is the temperature in degrees Celsius. (Note: The formula is an approximation at best and hold only fro specific temperature intervals.)

a. Find the number of matings when the temperature is 15 degrees Celsius.
b. Find the number of matings when the temperature is 25 degrees Celsius.
c. Find the rate of change of the number of matings when the temperature is 15 degrees Celsius.

The first two parts to this problem, a. and b, are relatively easy because we just want to plug in the different asked temperatures into t, our variable and solve.

a.
Plug this into a calculator: and the solution is about 3.385.
So, this means when the temperature is 15 degrees Celsius, the number of matings is about 3.

b.
Plug this into a calculator: and the solution is about 5.663.
So,, this means when the temperature is 25 degrees Celsius, the number of matings is about 6.

c. This is the most challenging part of the problem, and where the Calculus comes in. The directions ask us to find the RATE OF CHANGE of the number of matings when the temperature is 15 degrees Celsius. We know from previous posts that the rate of change is the derivative, so let’s differentiate.

First, we will re-write the original equation in exponential form.

Rewritten in exponential form:

Now, let’s take the derivative.

Now, let’s simplify:

Now, that we have the derivative, we will plug 15 in for t, and find the rate of change.

Plug the above values into a calculator, and you get approximately .22.
So, this means when the temperature is 15 degrees Celsius, the rate of change of the number of matings is about .22.

I hope you are beginning to see hoe Calculus can be used in everyday life!

Learn something new every day!

Kori 🙂

APPLES TO APPLES

Since I finally had the pleasure of getting to watch Jobs this weekend, staring one of my favs, Ashton Kutcher, I’m dedicating my post all about apples to a man who created one of the most magnificent companies, started out of garage, and very cleverly, but not really, named after the beloved fruit.

My last post dealt with finding absolute maximums and minimums of a function’s graph by evaluating the derivative. But, a question I am ready to take on in the classroom as a teacher, “Ms. Proffitt! When are we ever going to use this in the real world?!” This post will analyze a real life situation when knowing a min or max may benefit a real life BUSINESS situation. ( Jobs was really good at MAXAMIZING his profits as he once made $5000 of a project Atari paid him to do, and only paid the guy who really did it all for him $350, ouch.)

So, I have an Apple Orchard.

There are 50 apple trees in my orchard. Each tree produces 800 apples. For each additional tree planted, the output per tree drops by 10 apples. How many trees should be added to my orchard to maximize the total output of trees?

First, we want to make sure you know what the problem is asking you to find:
-We want to know the Maximum number of trees to be added to my orchard, which is my variable, to give me my Max number of Product, which is apples.
Next, let’s think about what the problem gives us. I currently have 50 trees that produce 800 apples each. That means right now, my MAX number of apples is 40,000.
-Also, we’re told that for each additional tree planted, my output decreases by 10 per tree.
-So, let’s try to use all this information to come up with some kinds of equation.

Second, let’s formulate the equation:
-I’m going to use P to stand for my Production, (In this case apples).
-What are we changing? That will be the variable, x, which in this case in the number of trees we’re adding.
-We are going to want to multiply our P= (total number of trees + the max amount of additional trees) (max possible apple output per tree, since that is decreasing by 10 per tree, we know we will need to use subtraction).
So, we could use an equation that looks like this in words.
P= ( # of trees)(Apples output per tree).
Now, let’s plug in everything we know.

Simplfy this:

Now, like we have learned before, to find an Absolute Max or Min, we must first find THE DERIVATIVE!!!!!

Let’s set the derivative equal to zero to find our critical value.

This is our critical value. This derivative tells us the maximum amount of trees I can have in my orchard to maximize my production of apples, which I can configure my simply inputting my x value I just found back into our original equation we created.

Therefore:


Therefore, the ABSOLUTE MAXIMUM number of apples my orchard can produce is 42,250 when my x-value of tree, which is the maximum amount I can have to continue to produce more apples than I already was is 15. So, if I plant 15 more trees, I can produce 2,250 more apples than with my original 50 trees where I was only producing 40,000 apples.

One may ask: well why wouldn’t I just keep planting more trees? If we plug 16, only one more tree back into our original equation, you get, P=42,240. This is 10 less apples than when we only plant 15 additional trees, and that is because of the part of the equation we included which subtracts 10 apples per additional tree. So we can plant a MAX of 15 more trees to MAXAMIZE the output of all the trees, which is indeed what the question initially asked us for!!! S

We better get to planting!!!

Learn something new everyday!!

Kori 🙂

Absolute Extrema

When you are looking at a graph, sometimes it is very easy to determine where the highest point is, what we will refer to as the absolute maximum, and the lowest point in the graph, which we will refer to as the absolute minimum.

For instance, the graphs below, which are all on a closed intervals, [a,b], each contain a maximum and a minimum.

The first graph in linear and contains a min at a and a max at b.
In the second graph, the max is between points a and b and the minimum is b.
The final graph shows the max and the min in between a and b.

So, you can also have a crazy graph with many dips and peaks. When a graph changes from increasing to deceasing, or vice versa, at a point with a horizontal slope, this is also known as a max or min, but these are referred to as relative maximums or relative minimums. Sometimes these same points are referred to as local max or mins.

In this post though we are focusing on the ABSOLUTE MAXIMUM and the ABSOLUTE MINIMUM, which are the highest and lowest y-values displayed on the graph. But, what if we are given a function without the accompaniment of a graph? How do we evaluate the absolute min and max then? YOU GUESSED IT!!!

BY USING THE DERIVATIVE, OF COURSE!!!!!

We could use a first derivative sign chart to help us begin, but ultimately, the chart gives us the zeros of the graph, and we still have to know if these zeros (critical values/horizontal tangent lines/points on the graph) are the absolute max and absolute min, as they could be just relative max or mins.

In order to do this, we are given a function, take the function’s derivative, set it equal to zero, solve, and then evaluate all the critical values and intervals inside the original equation to determine the highest and lowest output. Easier said than done, huh?

Let’s try some examples.

on the interval
Take the derivative.

Set the derivative equal to zero and solve.

Factor out a 3.




and
So, we have to test the critical values, which are our zeros, 1 and 3.
And, we have to test the interval values, 0 and 5.
Don’t forget! We are checking these values back in the ORIGINAL equation.

The original equation:

So, from this information, we can conclude the ABSOLUTE MAX is 12 when .
There are two values that produce the same minimum value, so we have two mins. The ABSOLUTE MIN is -8 when and when

Let’s do another:

on the interval
Take the derivative.

Set the derivative equal to zero.

Factor out 4x.





Therefore, this time our critical values to check are: 0,-4, and 4.
Don’t forget our interval values: -5 and 6.
AND–That’s right use the ORIGINAL FUNCTION!!

Therefore, the absolute maximum is 137 at x=6.
And, the absolute minimum is -263 when x=4 and x=-4.

Finally, let’s finish with one that is a little more challenging.

on the interval .
First, let’s take the derivative.
This function will need the use of the power rule and the chain rule to take the derivative.

Let’s rewrite our derivative, so that we put the negative exponent in the denominator of a fraction as we really don’t like working with negative exponents.

Doesn’t that just LOOK so much nicer!!
Now, set that REWRITTEN derivative equal to zero.

When we solve, we find that:
The absolute minimum is about 1.58 at x=0.
The absolute maximum is 2 at x=-2 and x=2.

Hey, it’s Sunday, I’m watching football, MY TEXANSSSS just got another touchdown, it’s the first day of my favorite month, lets do ONEEE MORE!

To take the derivative, use the quotient rule.

Simplify.



Set the numerator equal to zero.


The critical values are x=-1 and x=1.
Plug the critical values back into the original equation to find the absolute maximum and absolute minimum.
The absolute max is .5 when x=1.
The absolute min is -.5 when x=-1.

So, that is how you use a function’s derivative to identify the Absolute max and absolute min on a graph.

Learn something new every day!

Kori 🙂

Second Derivative Finds Concavity

The DERIVATIVE OF THE DERIVATIVE is called the SECOND DERIVATIVE.

Notated: , , or .

When the second derivative is positive, the original function is CONCAVE UP.
How do you remember this? “Concave up, like a CUP!”

When the second derivative is negative, the original function is concave down.
Is there a rhyme for this one too? “Concave down, like a FROWN!”

These little reminders will help you remember how we define concavity.

A function can have any combination of increasing/decreasing or concave up/ concave down.

The following pictures show examples of each.

Also, the second derivative and it’s sign chart will help us to find inflection points.
An inflection point is a point where the function changes CONCAVITY.
This graph shows a function with concavity that is UP then DOWN, and notice the inflection point (the point in which the concavity changes) is marked.

This graph shows concavity changing three times, therefore, there are three inflection points.

Let’s do an example:

The first step is to find the first derivative.

Then we will set the derivative equal to zeros and solve.


and .
We will then create a sign chart with the values found and determine from our chart if its increasing or decreasing.

Plot these points on a sign chart and determine which intervals are increasing or decreasing in between them.
First Derivative sign chart:

From our graph, we can conclude that the function is:
Increasing:
Decreasing:

Extrema:
The minimum is at x=-1.
The maximum is at x=6..

Finally, we will find the second derivative, and repeat the entire process which will help us determine concavity.
Use the first derivative to find the second derivative!!

Find the zeros.
.

Now, we will make another sign chart for the second derivative to determine concavity and inflection points, if there are any.
Second Derivative Sign Chart:

Recall: When the second derivative is negative, it is concave down, and when the second derivative is positive it is concave up.
Concave down:
Concave up:
Last, the inflection points, there is only one, and remember this is the point where concavity changes.
The inflection point is as this is the point where the function changes from concave down to concave up.

I hope sign charts are helping you to learn and understand all this valuable information that first and second derivatives can show you!!

Learn something new everyday!

Kori 🙂

Using the First Derivative to find out more!

Once you take the derivative of a function, you can use that information to create a sign chart that will easily identify for you where the function is increasing or decreasing and local extrema. (Min and max)

If the first derivative is positive, then the function is increasing.
If the first derivative is negative, then the function is decreasing.

For example:

The derivative is:

Now, we will use the first derivative to find the zeros of the function.
First, we will factor out and get This is a difference of 2 squares, so it factors nicely.

Set each piece equal to 0.
Our three zeros equal:

Now, we can make our sign chart and determine when the function is increasing or decreasing.

To determine whether or not the function is increasing or decreasing, we plug in any numbers in between our intervals of zeros to determine if the result it positive or negative.

So, in this function:
Decreasing:
Increasing:

Extrema:
The minimum, there are two are at: x=3 and x=-3.
The maximum is at x=0.

So, we can determine all this information by taking the first derivative of the function, finding the zeros, making a sign chart, then plug in values to determine if negative or positive, (increasing or decreasing).

Hope this was interesting!!

Learn something new every day,

Kori 🙂

A Post with Many Examples Using Multiple Rules

In the first problem, we will use the product and the quotient rule!

Let’s be reminded of these rules:
Product:
Quotient:

We will first use the product rule to find the derivative of the “top” or the numerator. And then use that derivative inside the quotient rule.
So, the derivative of just the top=
Now, plug that into our quotient rule with our more simple derivative.
The derivative of the bottom is simply 5.

Simplify by multiplication and addition.



Combine like terms.

This problem will require the use of the chain rule and the quotient rule.

In this problem we will use the chain rule within the quotient rule. This chain rule is needed to determine the derivative of the numerator. Once we find the derivative of the numerator from the chain rule, we plug in our values and derivatives to the easy quotient rule and simplify.

Here’s another example, using the product rule combined with the quotient rule:

Once again, the product rule is used within the quotient rule, and should be found first.
The derivative of the top based on the product rule=
Then plug in this derivative and the derivative of the bottom which is equal to 7 to the quotient rule.

This function will require the use of the chain rule and the quotient rule!

And these examples are the various ways you can use multiple rules to solve for the derivative.

Learn something new everyday,

Kori 🙂