Second Derivative Finds Concavity

The DERIVATIVE OF THE DERIVATIVE is called the SECOND DERIVATIVE.

Notated: , , or .

When the second derivative is positive, the original function is CONCAVE UP.
How do you remember this? “Concave up, like a CUP!”

When the second derivative is negative, the original function is concave down.
Is there a rhyme for this one too? “Concave down, like a FROWN!”

These little reminders will help you remember how we define concavity.

A function can have any combination of increasing/decreasing or concave up/ concave down.

The following pictures show examples of each.

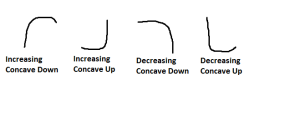
Also, the second derivative and it’s sign chart will help us to find inflection points.
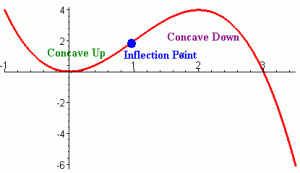
An inflection point is a point where the function changes CONCAVITY.
This graph shows a function with concavity that is UP then DOWN, and notice the inflection point (the point in which the concavity changes) is marked.

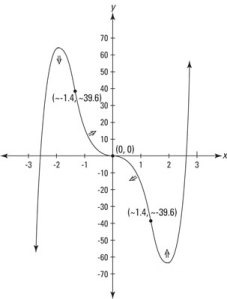
This graph shows concavity changing three times, therefore, there are three inflection points.

Let’s do an example:

The first step is to find the first derivative.

Then we will set the derivative equal to zeros and solve.


and .
We will then create a sign chart with the values found and determine from our chart if its increasing or decreasing.

Plot these points on a sign chart and determine which intervals are increasing or decreasing in between them.
First Derivative sign chart:

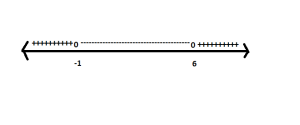
From our graph, we can conclude that the function is:
Increasing:
Decreasing:

Extrema:
The minimum is at x=-1.
The maximum is at x=6..

Finally, we will find the second derivative, and repeat the entire process which will help us determine concavity.
Use the first derivative to find the second derivative!!

Find the zeros.
.

Now, we will make another sign chart for the second derivative to determine concavity and inflection points, if there are any.
Second Derivative Sign Chart:

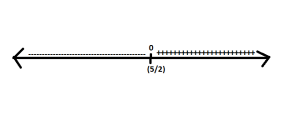
Recall: When the second derivative is negative, it is concave down, and when the second derivative is positive it is concave up.
Concave down:
Concave up:
Last, the inflection points, there is only one, and remember this is the point where concavity changes.
The inflection point is as this is the point where the function changes from concave down to concave up.

I hope sign charts are helping you to learn and understand all this valuable information that first and second derivatives can show you!!

Learn something new everyday!

Kori 🙂

About koriproffitt

I am a Senior at Texas State University. I am majoring in Education, and graduate in December!

View all posts by koriproffitt →